Gradient Boosting on Titanic Data

1. Predicting Age

1.1 Import the data

import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
np.random.seed(12356)
df = pd.read_csv('titanic.csv')
df = df.dropna()

1.2 Assign input and output variabble

# Assign input variables
X = df.loc[:,['Pclass','Sex','Fare','Embarked','SibSp','Parch','Survived']]

# Assign target variable
y = df['Age']

1.3 Handle some missing and fix variables types

# Impute the Embarked variable
X["Embarked"] = X["Embarked"].fillna("S")
# Change Pclass to categorical variable
X['Pclass'] = X['Pclass'].astype(object)
X['Survived'] = X['Survived'].astype(object)

1.4 Encode categorical variable

X = pd.get_dummies(X)

1.5 Split the data

from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(X,y,test_size=0.3)

1.6 Set up and Train Gradient Boosting

from sklearn.ensemble import GradientBoostingRegressor
r1 = GradientBoostingRegressor(n_estimators=100, learning_rate=1)
r1.fit(x_train, y_train)

# Rsquared
from sklearn.metrics import r2_score
print('Rsquared on Testing: ', r2_score(y_test, r1.predict(x_test)))

Rsquared on Testing:  -0.5469087105560149

Variable Importance

import warnings
warnings.filterwarnings('ignore')

sorted_idx = (-r1.feature_importances_).argsort()

feature_importance = pd.DataFrame({'Variables':x_train.columns[sorted_idx], 'Importance':r1.feature_importances_[sorted_idx]})
df = feature_importance[:10]
df.sort_values('Importance',inplace=True)

df.plot(kind='barh',y='Importance',x='Variables', legend=False)

<Axes: ylabel='Variables'>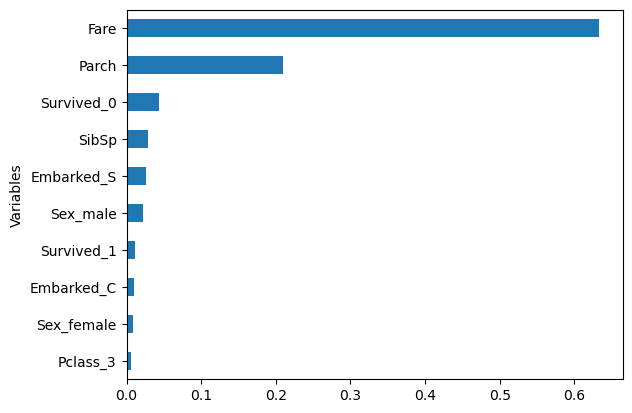

# Plot the Training Accuracy of gradient boosting with n_estimators running from n1 to n2 and two learning rates l1 and l2. 

n1 = 1
n2 = 100
l1 = .1
l2 = 1

ac = pd.DataFrame([], columns=list(['Rounds','Learning Rate','Testing Rsquared']))

for rs in range(n1, n2):
    for lr in [l1, l2]:
        boost = GradientBoostingRegressor(n_estimators=rs, learning_rate=lr)
        boost.fit(x_train,y_train)
        
        ac = pd.concat([ac, pd.DataFrame([[rs, lr, boost.score(x_train, y_train)]], 
                                    columns=list(['Rounds','Learning Rate','Train Rsquared']))], 
                       ignore_index=True)
        

import seaborn as sns; sns.set()
import matplotlib.pyplot as plt
ax = sns.lineplot(x="Rounds", y="Train Rsquared", hue =ac['Learning Rate'].astype('category'),data=ac)
ax.text(x=0.5, y=1.1, s='Learning fast vs. Learning slow', fontsize=16, weight='bold', ha='center', va='bottom', transform=ax.transAxes)

Text(0.5, 1.1, 'Learning fast vs. Learning slow')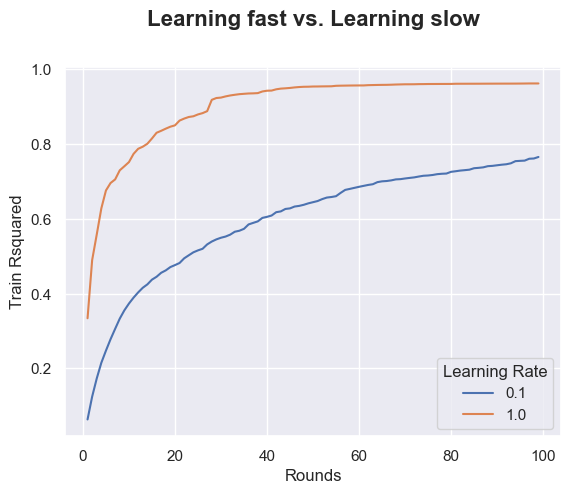

# Plot the Training Accuracy of gradient boosting with n_estimators running from n1 to n2 and two learning rates l1 and l2. 

n1 = 1
n2 = 100
l1 = .1
l2 = 1

ac = pd.DataFrame([], columns=list(['Rounds','Learning Rate','Testing Rsquared']))

for rs in range(n1, n2):
    for lr in [l1, l2]:
        boost = GradientBoostingRegressor(n_estimators=rs, learning_rate=lr)
        boost.fit(x_train,y_train)
        
        ac = pd.concat([ac, pd.DataFrame([[rs, lr, boost.score(x_test, y_test)]], 
                                    columns=list(['Rounds','Learning Rate','Testing Rsquared']))], 
                       ignore_index=True)
        

import seaborn as sns; sns.set()
import matplotlib.pyplot as plt
ax = sns.lineplot(x="Rounds", y="Testing Rsquared", hue =ac['Learning Rate'].astype('category'),data=ac)
ax.text(x=0.5, y=1.1, s='Learning fast vs. Learning slow', fontsize=16, weight='bold', ha='center', va='bottom', transform=ax.transAxes)

Text(0.5, 1.1, 'Learning fast vs. Learning slow')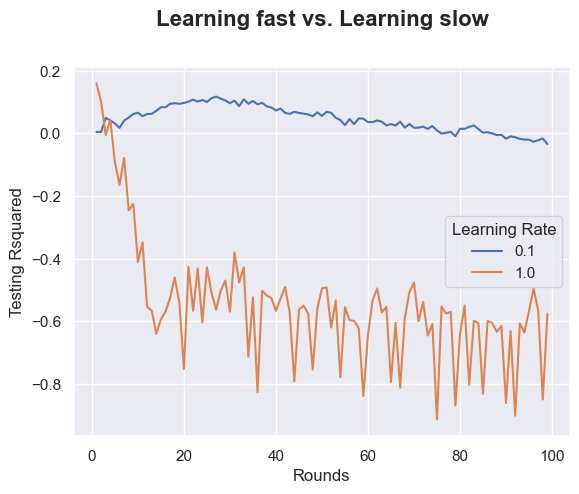

2. Practice

Predicting NBA Salary. Download the data at: https://bryantstats.github.io/math460/python/nba_salary.csv

1. Import the data and drop all the missing values

2. Set the input (X) and output (y) (Use df.columns to see all the columns to easier copy/paste). Split the data into 60% training and 40% testing (No need to do 1.3 and 1.4 as all variables are numeric and have correct types)

3. Train an gradient boosting with 200 n_estimators and .1 learning_rare. What is testing Rsquared of the gradient boosting?

4. What is the most important variable according to the above gradient boosting model?

5. Find an gradient boosting (try a few different of n_estimators and learning_rate) that have a higher testing Rsquared than the above gradient boosting. What is the n_estimators and learning of this gradient boosting?